Stanisław Ulam, przedstawiciel słynnej polskiej przedwojennej lwowskiej szkoły matematycznej, wybitny matematyk i naukowiec, w roku 1939 wyjechał do USA i pozostał tam na stałe. Był uczestnikiem Projektu Manhattan i współtwórcą pierwszej bomby atomowej. Tenże Ulam, jak głosi Wikipedia, w roku 1963 nudząc się na jakimś mało interesującym wykładzie, zaczął rysować na kartce kolejne liczby w formie spirali. Zapewne wyglądało to mniej więcej tak jak na grafice poniżej:

Wyróżniając na diagramie liczby pierwsze, już przy całkiem niedużych obszarach można zauważyć, że rozkład tych liczb nie jest zupełnie przypadkowy. Mianowicie liczby pierwsze, co oczywiste występują na przekątnych nieparzystych (poza 2 są liczbami nieparzystymi) ale co ciekawe, niektóre przekątne są zdecydowanie bardziej preferowane od pozostałych. Po raz kolejny w historii matematyki coś zasugerowało, że rozkład liczb pierwszych pośród pozostałych liczb może opisywać jakaś reguła.

Rysowanie diagramów aż się prosiło o zastosowanie komputerów, co też szybko uczyniono i w sieci można znaleźć wiele ciekawych wizualizacji diagramów. Ja wybrałem sobie to zadanie jako inspirujący temat do nauki Pythona. Liczby pierwsze łatwo i szybko wyznacza się jednym ze starszych algorytmów ludzkości, czyli za pomocą sita Erastotenesa.

Bierzemy podzbiór liczb naturalnych [0,maxn], z którego chcemy wybrać liczby pierwsze. zaczynamy od 2 i w pierwszej kolejności wykreślamy ze zbioru wszystkie wielokrotności liczby 2 większe od niej samej, bo nie są one liczbami pierwszymi. W następnym kroku bierzemy kolejną nie wykreślona liczbę ze zbioru, w tym wypadku 3 i wykreślamy je dalsze wielokrotności. Dalej bierzemy kolejną nie wykreśloną (5) itd. Algorytm zatrzymujemy w momencie kiedy liczba której wielokrotności chcemy wykreślać będzie większa od √maxn.

W tym miejscu należy się krótka wzmianka o autorze algorytmu. Erastotenes był grekiem, który w III w. p.n.e. żył w Aleksandrii i zarządzał tamtejszą biblioteką, będącą zbiorem większości wiedzy naukowej jaką w tamtych czasach znała ludzkość. Poza algorytmem wyznaczania licz pierwszych jego autor znany jest między innymi z najstarszego, znanego współcześnie, trafnego oszacowania wielkości kuli ziemskiej. Szacowania wykonanego za pomocą reguł geometrii, kijka rzucającego cień i pomiaru odległości z Aleksandrii do Syene (około 800km) w krokach. Przy tak prostych środkach wyznaczył promień krzywizny powierzchni Ziemi i jej rozmiaru z błędem nie przekraczającym kilku procent. To jego zachowane dzieła, w których twierdził że można płynąc na zachód dotrzeć do Indii, po ponad 1600 latach pomogły zainspirować Kolumba do jego wyprawy.

Wracając do liczb pierwszych, do wizualizacji wyników wybrałem, sugerując się podpowiedziami wujka Google, bibliotekę matplotlib. Wynik mojego pierwszego skryptu poniżej, spirala Ulama w przestrzeni 601 na 601, czyli wszystkie liczby pierwsze od 2 do 361183.

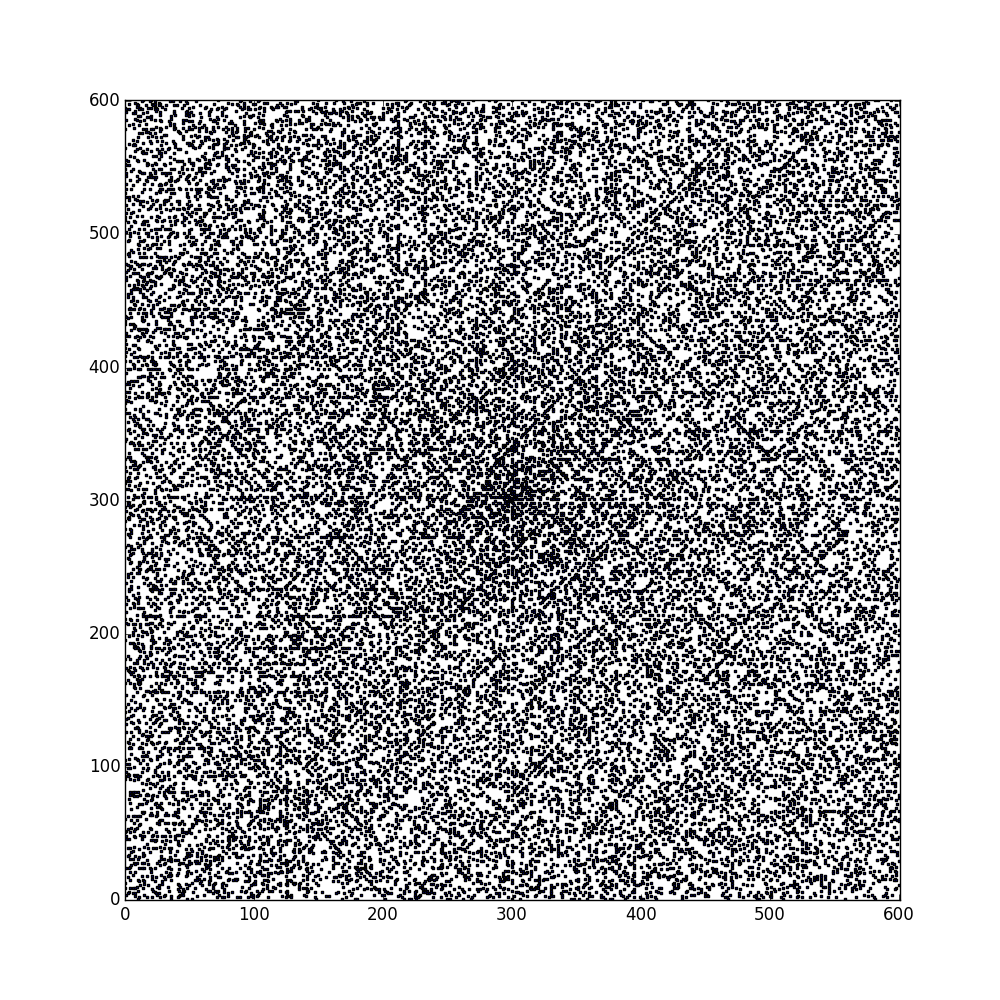
Mało? To tak wygląda spirala o znacznie większym rozmiarze: Spirala licz pierwszych

W kolejnym podejściu postanowiłem zobaczyć jak to wygląda jeżeli nie będziemy zaczynać spirali od jedynki tylko od kolejnych liczb naturalnych. Między innymi powstała następująca animacja obrazująca wygląd spirali dla liczb początkowych od 1 do 1000.

I kolejny film, obszar 100 na 100, zaczynamy spiralę od 1 do 3000.

Skrypt Python 3.x do generowania animowanych spirali Ulama  można pobrać z repozytorium GitHub https://github.com/majchernet/animated-ulam-spiral-generator.

Spirale Roberta Sacksa

Równie ciekawy, jak nie ciekawszy efekt wizualizacji rozkładu liczb pierwszych, możemy uzyskać po użyciu współrzędnych radialnych. Spirale takie noszą imię Roberta Sacksa i wyglądają jak na przykładzie poniżej:

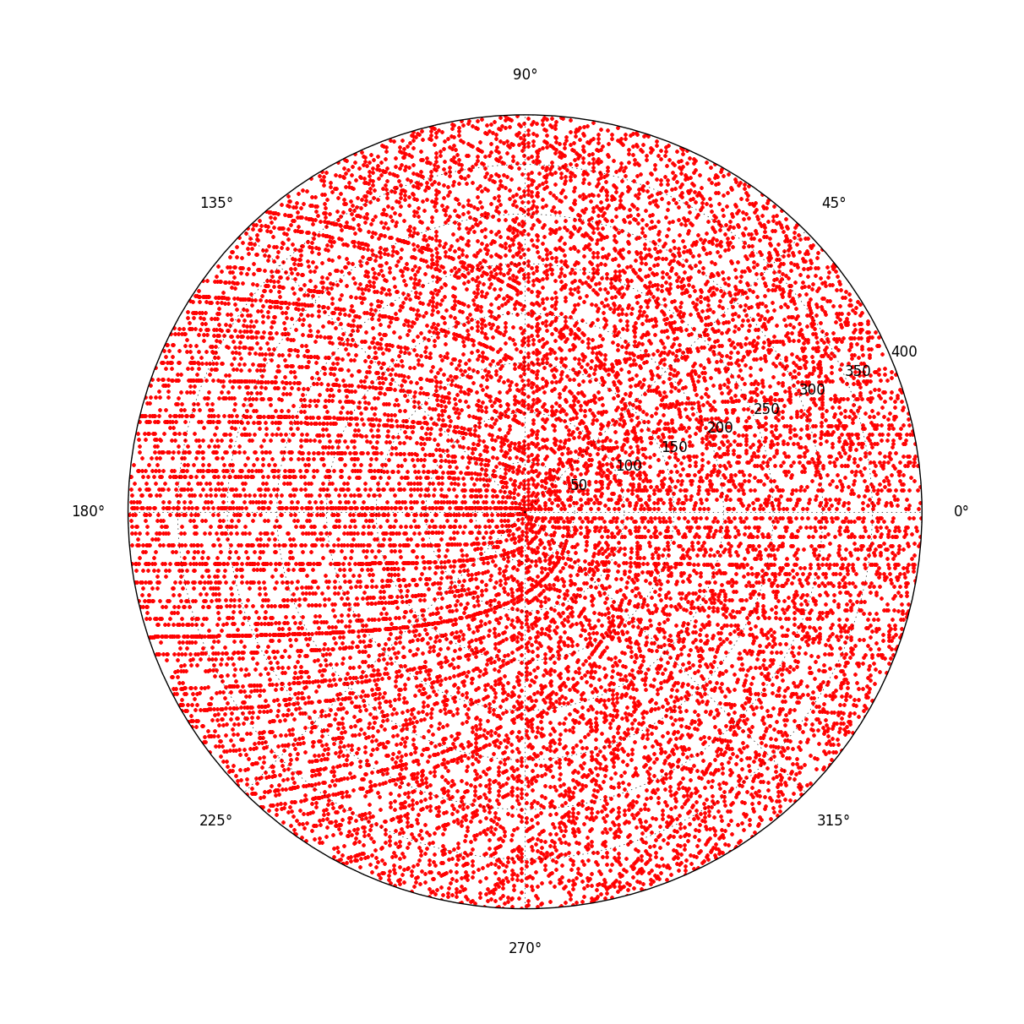
Podobnie jak dla spiral Ulama również te możemy rozpoczynać od kolejnych licz uzyskując animację jak poniżej.

Jak uprzednio liczby pierwsze wydają się nie występować zupełnie losowo. Upodobały sobie niektóre „linie”. Te widoczne na diagramie linie wyznaczone są przez funkcje wielomianowe, w tym wypadku znaną nam dobrze ze szkoły rodzinę funkcji kwadratowych a₂x²+a₁x+a₀=0 Jeden z tych wielomianów (x²+x+41=0), na długo przed odkryciem samych diagramów, został opisany w 1772 roku przez Eulera, który jak wiadomo, wielkim matematykiem był. Poniżej wizualizacja na niebiesko wartości tego wielomianu dla dziedziny liczb naturalnych, które są liczbami pierwszymi.

Zobaczmy jak to wygląda na animacji. Poniżej animacja (dla 500k) z zaznaczonymi 100 najbardziej „skutecznymi wielomianami.