W 1772 Eulera opisał wielomian (n2+n+41=0), jako stosunkowo sprawnie wyznaczający liczby pierwsze w dziedzinie liczb naturalnych. Mając podany na tacy przez Wielkiego Matematyka taki ładny wielomian, który tak pięknie prezentuje się na spirali Roberta Sacksa, nie mogłem się oprzeć przed zatrudnieniem mojego RTX’a do sprawdzenia kilku jego początkowych wartości. Późnym wieczorem odpaliłem program, który był lekko zoptymalizowany pod CUDA NVIDI. Kto ma dzieci tego nie dziwi, że można wstać od komputera w piątek i wrócić do niego dopiero w poniedziałek. Tak więc kilka kWh później wyskoczyła mi tytułowa liczba. Jak będziecie się kiedyś zastanawiać czy 4000002000041 jest liczbą pierwszą, to wygląda na to że jest. Jest to wartość wielomianu dla 2 000 000. A jak wyglądają wszystkie mniejsze od niej liczby pierwsze, które są wartościami wielomianu Eulera w dziedzinie liczb naturalnych? To można zobaczyć w tym pliku (11MB):
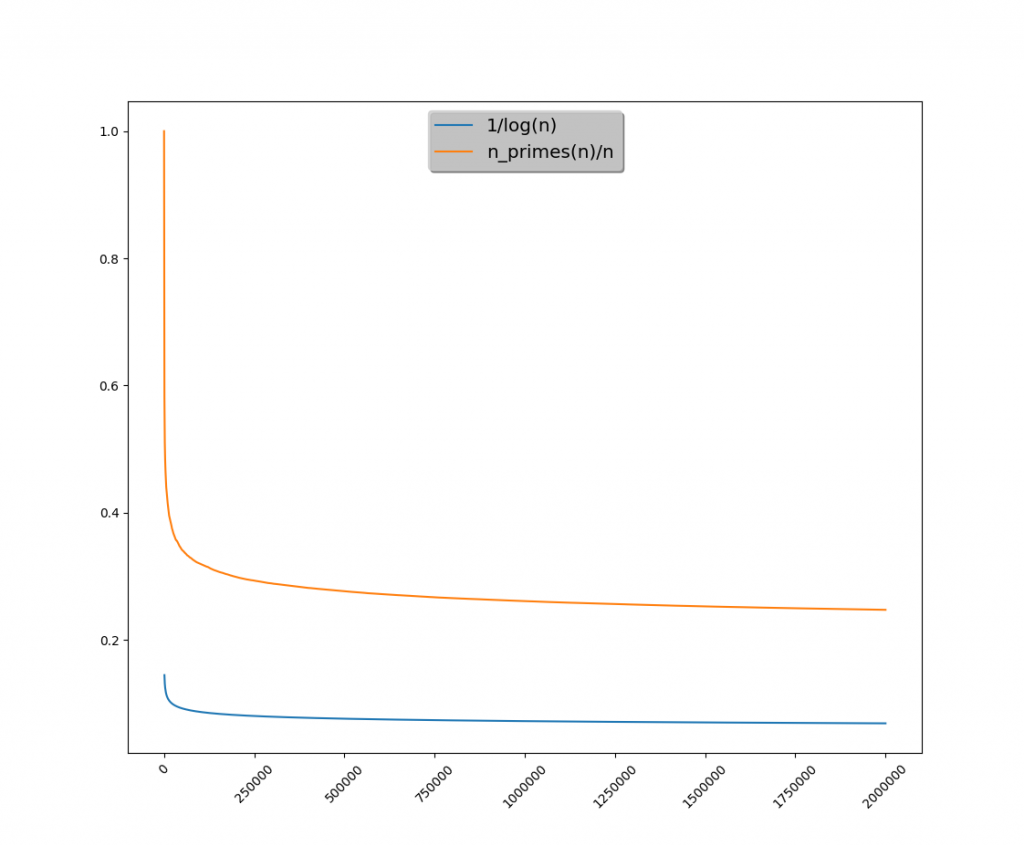
Gęstość liczb pierwszych w zbiorze liczb naturalnych 1..N dla dużych N wyznacza funkcja π(N) ~ N/log(N), czyli liczby pierwsze stanowią 1/log(N) części zbioru. Log to logarytm naturalny, w czasach mojej edukacji zapisywany jako ln. Taką samą kalkulację możemy przeprowadzić dla naszego zbioru liczb wyznaczonych przez wielomian Eulera. Stosunek ilości liczb pierwszych do wszystkich wartości dla liczb naturalnych w zakresie 1..N przy N = 2 000 000 – do której to wartości doliczyłem – wynosi 0.247394. W zakresie do N = 39 jest to 100%, czyli trafności generowania liczby przez wielomian Eulera w tym przedziale wynosi 1.





Chciałbym zauważyć, że wielomian ten generuje liczby pierwsze do wartości n=41. Później generowane liczby mogą być liczbami pierwszymi, ale nie muszą. Trzeba sprawdzić ich 'pierwszość’ tradycyjnymi metodami … niestety. Eksperyment godny naśladowania, chyba też spróbuję. Pozdrawiam
Oczywiście jest tak jak Pan pisze. Trzeba robić faktoryzację dla każdej kolejnej wartości wielomianu, żeby potwierdzić lub zaprzeczyć jej pierwszości. Dlatego proces liczenia zajął ponad dwie doby. Wartości wielomianu, które są liczbami pierwszymi znajdują się w pliku https://majcher.net/wp-content/uploads/2020/10/euler_polynomial_pn.txt (n^2-n+41, daje liczby pierwsze dla n w zakresie <0,39>, potem gęstość spada).