Ponad 108 lat temu, w piątym dniu po oddaniu do eksploatacji, w trakcie swojego dziewiczego rejsu, po zderzeniu z górą lodową w dniu 15 kwietnia 1912 roku zatonął RMS Titanic. Katastrofa ta pochłonęła życie ponad 1500 ofiar, które utonęły bądź zmarły w wyniku hipotermii w lodowatych wodach Północnego Atlantyku. Wśród nich było wiele rodzin wraz z dziećmi, które wyruszyły do Ameryki w poszukiwaniu lepszej przyszłości. To im dedykuję ten wpis.

Katastrofa Titanic’a wpisała i mocno utrwaliła się w kulturze masowej krajów zachodu. Pomimo że zdarzyły się w historii większe katastrofy morskie, jak np. zatopiony w 1945 na Bałtyku MV Wilhelm Gustloff, to o Titanicu słyszał i wie prawie każdy. Jedną z pozostałości po tym wydarzeniu, jest lista pasażerów feralnego rejsu, która stała się bazą edukacyjnego zadania konkursowego na platformie Kaggle. Zadanie polega na tym, by na podstawie części treningowych danych, nauczyć algorytm przewidywania kto przeżył katastrofę.
Lista pasażerów została podzielona na dwie części. Listę „train” zawierająca informacje czy ktoś przeżył oraz listę „test”, którą musimy o tę informację uzupełnić naszym algorytmem. Walidacja i ocena naszego algorytmu odbywa się na podstawie dokładności z jaką wykonana została predykcja. Kilka lat temu poświęciłem sporo czasu temu zadaniu w trakcie nauki algorytmów uczenia maszynowego a ten tekst, jest jednym z wielu zaległych, które postanowiłem kiedyś o tym napisać.
Zadanie jest przypadkiem uczenia nadzorowanego i problemu klasyfikacji, mamy przekazane dane do wyćwiczenia naszego algorytmu i powiązaną z nimi zmienną wyjaśnianą (Survived), która przyjmuje dwie wartość 0 lub 1. Zaczynamy od wczytania danych treningowych do Pandas DataFrame i ich wstępnej analizy. Dane są zapisane w formie pliku CSV.
import numpy as np
import pandas as pd
train_data = pd.read_csv("data/train.csv")
Szybkie spojrzenie na przykładowe dane:
In [8]: train_data.head(5) Out[8]: PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket Fare Cabin Embarked 0 1 0 3 Braund, Mr. Owen Harris male 22.0 1 0 A/5 21171 7.2500 NaN S 1 2 1 1 Cumings, Mrs. John Bradley (Florence Briggs Th... female 38.0 1 0 PC 17599 71.2833 C85 C 2 3 1 3 Heikkinen, Miss. Laina female 26.0 0 0 STON/O2. 3101282 7.9250 NaN S 3 4 1 1 Futrelle, Mrs. Jacques Heath (Lily May Peel) female 35.0 1 0 113803 53.1000 C123 S 4 5 0 3 Allen, Mr. William Henry male 35.0 0 0 373450 8.0500 NaN S
Mamy kolejno takie informacje jak: id pasażera, czy przeżył katastrofę czyli naszą zmienną wyjaśnianą, klasa którą podróżował, imię i nazwisko, płeć, wiek, rodzina „pozioma” na pokładzie tj. rodzeństwo i małżonkowie, rodzina „pionowa” na pokładzie tj. rodzice i dzieci, numer biletu, cena biletu, numer kabiny, port zaokrętowania.
Na początek spójrzmy na to co się często powtarza o przetrwałych zatonięcie Titanica czyli, że przeżyli głownie bogaci, kobiety i dzieci. Poniżej proste wizualizacje dla części danych. Tu należy się mała dygresja, wykresy te wygenerowałem za pomocą wspaniałego oprogramowania https://www.dataiku.com/, które polecił mi mój kolega Marek. Dzięki temu wróciłem do tematu Titanica i dlatego możecie przeczytać ten wpis.
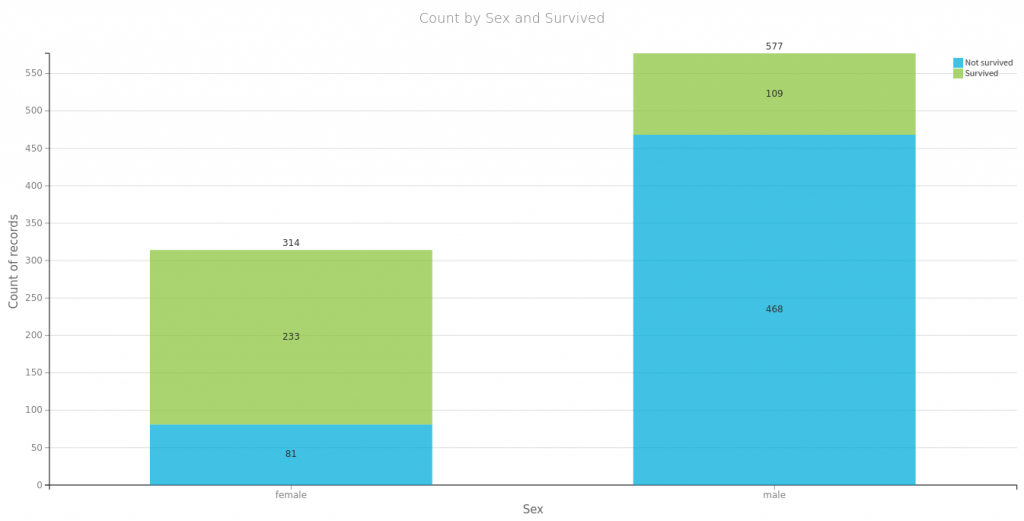
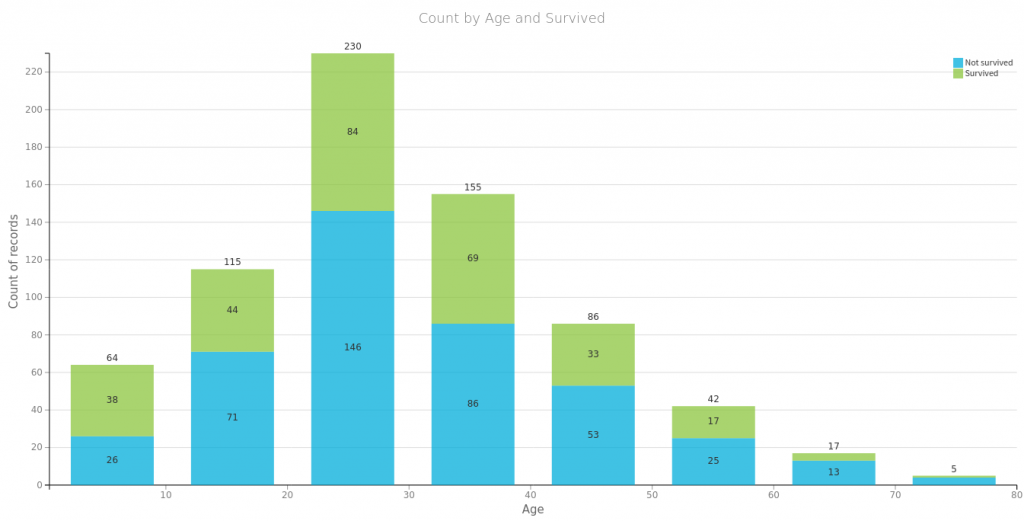
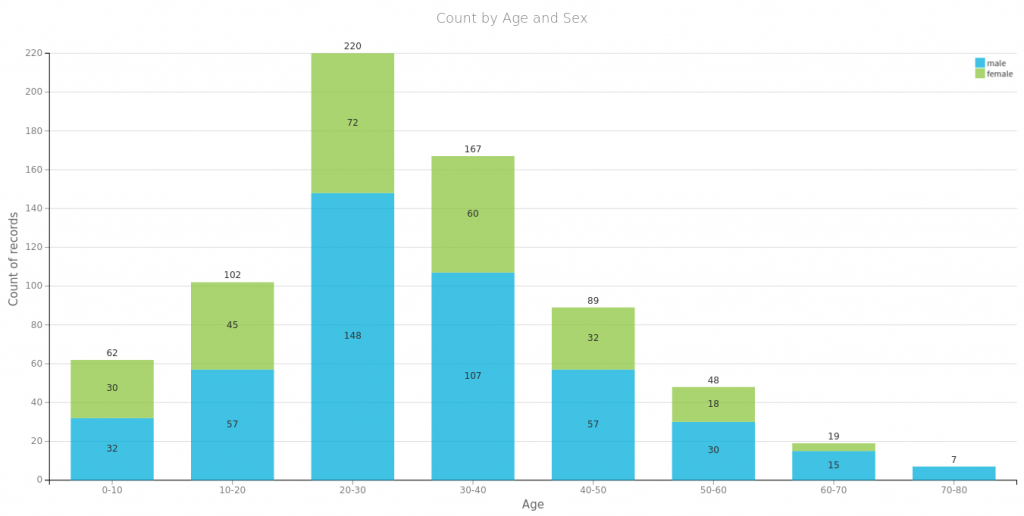
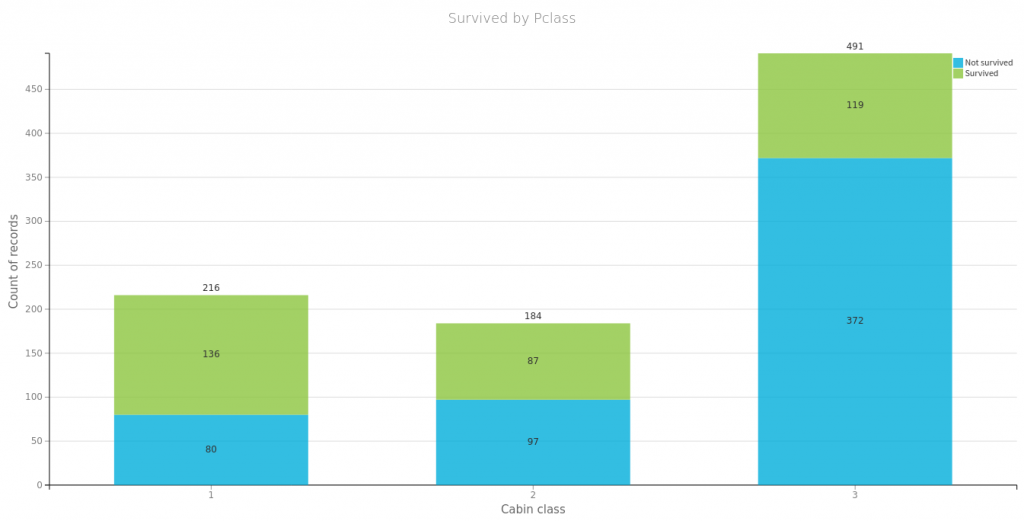
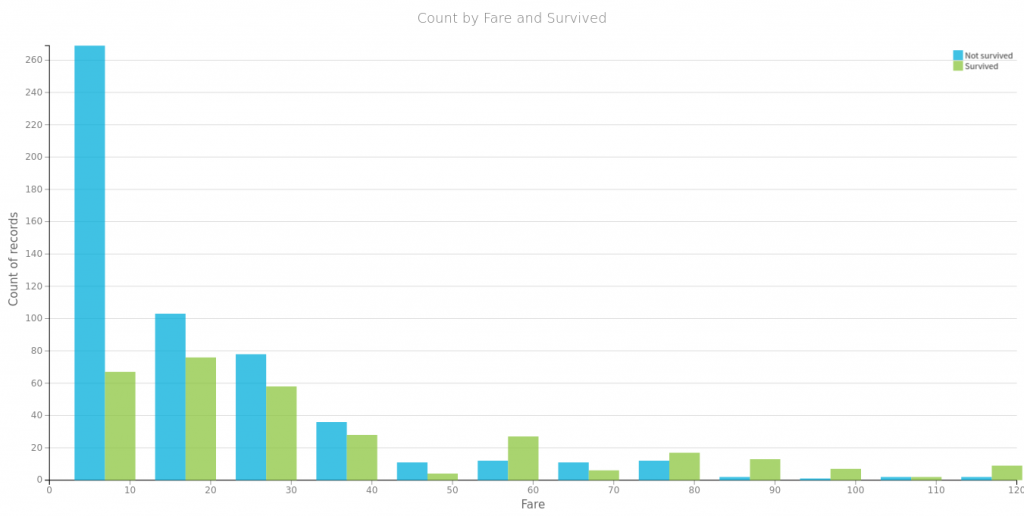
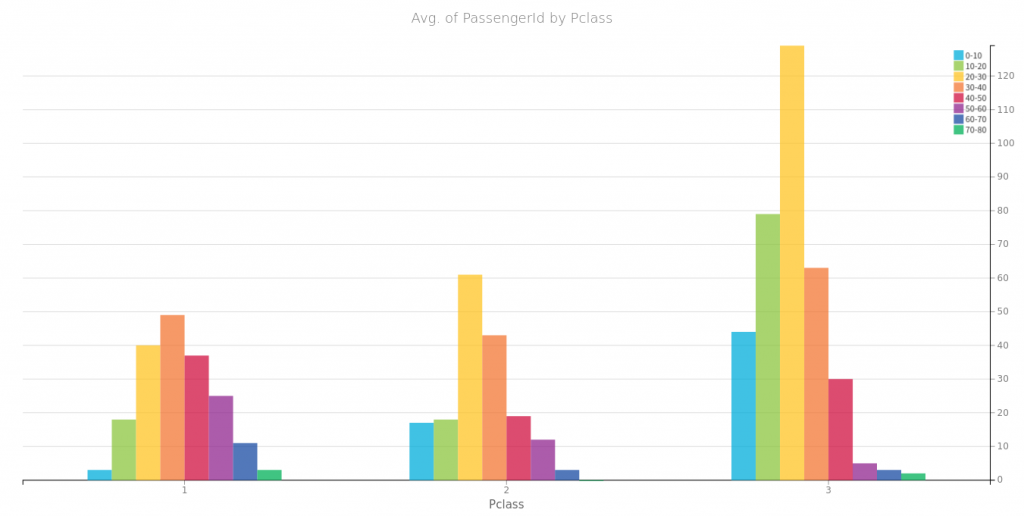
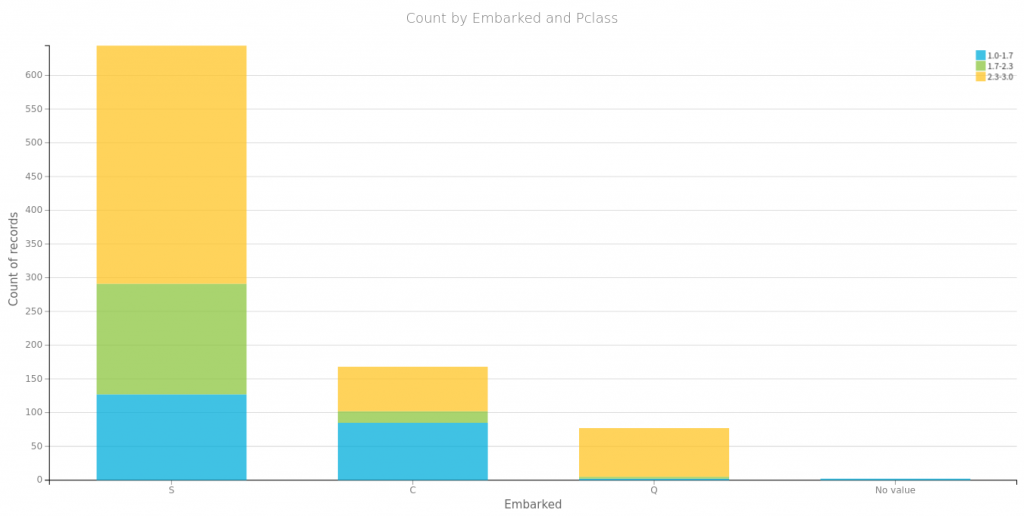
Płeć i miejsce zaokrętowania, jako zmienne które przyjmują wzajemnie wykluczające się wartości, możemy zamienić na wektory typu one-hot:
dummies = pd.get_dummies(train_data['Sex'], prefix='Sex', prefix_sep='-') train_data = pd.concat([train_data, dummies], axis=1) dummies = pd.get_dummies(train_data['Embarked'], prefix='Embarked', prefix_sep='-') train_data = pd.concat([train_data, dummies], axis=1) train_data.drop(['Sex','Embarked'], axis=1, inplace=True)
Następnie sprawdźmy ile danych nie ma podanych wartości:
In [10]: train_data.isna().sum() Out[10]: PassengerId 0 Survived 0 Pclass 0 Name 0 Age 177 SibSp 0 Parch 0 Ticket 0 Fare 0 Cabin 687 Sex-female 0 Sex-male 0 Embarked-C 0 Embarked-Q 0 Embarked-S 0 dtype: int64
Kabiny możemy się spokojnie pozbyć z danych a wiek spróbujemy uzupełnić na podstawie ilości członków rodziny. W tym celu grupujemy dane po liczbie krewnych w kolumnach 'Parch’ i 'SibSp’ i wyliczamy medianę dla każdej z grup oraz potrzebna później medianę wieku dla wszystkich pasażerów zbioru treningowego:
In [14]: age_medians = train_data.groupby(['Parch', 'SibSp'])['Age'].median()
In [15]: age_median = train_data['Age'].median()
In [16]: age_medians
Out[16]:
Parch SibSp
0 0 29.5
1 30.0
2 28.0
3 31.5
1 0 27.0
1 30.5
2 4.0
3 3.0
4 7.0
2 0 20.5
1 24.0
2 19.5
3 10.0
4 6.0
5 11.0
8 NaN
3 0 24.0
1 48.0
2 24.0
4 0 29.0
1 45.0
5 0 40.0
1 39.0
6 1 43.0
Name: Age, dtype: float64
In [17]: age_median
Out[17]: 28.0
Sprawdzamy po kolei nasze dane i w przypadku braku wieku pasażera uzupełniamy go o medianę wieku z grupy o takim samym składzie rodzinnym. W przypadku braku takiej mediany (np. parch-sibsp 2-8) uzupełniamy wartością mediany dla wszystkich danych.
for i, row in train_data.iterrows():
if row['Age'] != row['Age']:
guess_age = age_medians[row['Parch'],row['SibSp']]
if guess_age != guess_age:
guess_age = age_median
train_data.at[i, 'Age'] = guess_age
Usuwamy pozostałe nieprzydatne dla algorytmu zmienne tj. numer pasażera, imię i nazwisko, numer biletu i numer kabiny. Następnie sprawdźmy jak pozostałe zmienne skorelowane są ze zmienną wyjaśnianą 'Survived’
In[18]: train_data.drop(['PassengerId','Name','Ticket','Cabin'], axis=1, inplace=True) ...: train_data.corr()['Survived'] Out[18]: Survived 1.000000 Pclass -0.338481 Age -0.059508 SibSp -0.035322 Parch 0.081629 Fare 0.257307 Sex-female 0.543351 Sex-male -0.543351 Embarked-C 0.168240 Embarked-Q 0.003650 Embarked-S -0.155660 Name: Survived, dtype: float64
Najbardziej znaczące są płeć, cena i klasa biletu. Wiek i krewni nie mają zbyt dużej korelacji z faktem przeżycia. Wysoka korelacja miejsca zaokrętowania wynika zapewne z nierównego rozłożenia na klasy pasażerów wsiadających w poszczególnych portach (wykres powyżej). Płeć jako binarną możemy spokojnie usnąć dla jednej z przyjmowanych wartości. Pozostałe dane ujednolicamy za pomocą normalizacji min-max.
train_data.drop(['Sex-male'], axis=1, inplace=True) from sklearn.preprocessing import MinMaxScaler scaler = MinMaxScaler() to_scale = ['Fare','Age','Parch','SibSp','Pclass'] train_data[to_scale] = scaler.fit_transform(train_data[to_scale])
Mamy przygotowane dane do zasilenia algorytmu predykcji. W celu oceny skuteczności naszej klasyfikacji pasażerów, dostępne dane treningowe musimy podzielić sobie na dwie części, cześć do nauki algorytmu oraz na cześć do oceny jego skuteczności, czyli tzw. zbiór 'cross validation’. Dzielimy nasze dane w stosunku 8 do 2. Jedna piąta losowo wybranych rekordów będzie stanowiła zbiór służący do walidacji i oceny działania algorytmu.
from sklearn.model_selection import train_test_split train, cv = train_test_split(train_data, test_size=0.2)
Zmienną wyjaśnianą 'Survived’ mamy w pierwszej kolumnie otrzymanych zbiorów cv i train. Rozdzielamy zmienne wyjaśniane od wyjaśniających (features od labels).
train_data_f = train.iloc[:,1:] train_data_l = train.iloc[:,0] cv_data_f = cv.iloc[:,1:] cv_data_l = cv.iloc[:,0]
Na tak przygotowanych danych przetestujemy kilka klasyfikatorów żeby wybrać ten, który jest najbardziej skuteczny.
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB
classifiers = [['RFC',RandomForestClassifier()],
['GBC',GradientBoostingClassifier()],
['LR',LogisticRegression()],
['KNN',KNeighborsClassifier(n_neighbors=7)],
['SVC',SVC()],
['GNB',GaussianNB()]]
for classifier in classifiers:
classifier[1].fit (train_data_f,train_data_l)
print ("{}:\t{}".format(classifier[0],classifier[1].score(cv_data_f,cv_data_l)))
Tych kilka subiektywnie wybranych klasyfikatorów, bez strojenia ich parametrów, daje przykładowy wynik dla metryki opartej na dokładności (accuracy):
RFC: 0.8156424581005587 GBC: 0.8603351955307262 LR: 0.8324022346368715 KNN: 0.8547486033519553 SVC: 0.8212290502793296 GNB: 0.7374301675977654
Należy pamiętać, że zbiory do nauki i walidacji klasyfikatorów dobierane są losowo, więc za każdym uruchomieniem będziemy mieli różne wyniki. Dla pewności przetestujemy każdy klasyfikator 100 razy i wyliczymy średnią z uzyskanych wyników.
results = pd.DataFrame(columns=([c[0] for c in classifiers]))
for i in range (0,100):
train, cv = train_test_split(train_data, test_size=0.2)
train_data_f = train.iloc[:,1:]
train_data_l = train.iloc[:,0]
cv_data_f = cv.iloc[:,1:]
cv_data_l = cv.iloc[:,0]
acclist = []
for classifier in classifiers:
classifier[1].fit (train_data_f,train_data_l)
accuracy = classifier[1].score(cv_data_f,cv_data_l)
acclist.append(accuracy)
results.loc[len(results)] = acclist
print (results.mean())
RFC 0.804478
GBC 0.821343
LR 0.791269
KNN 0.797948
SVC 0.806754
GNB 0.776940
dtype: float64
Najlepszy w takim minimalistycznym podejściu okazuję się GradientBoostingClassifier, którego użyjemy do predykcji dla danych testowych. Zapamiętamy nasz wygrany klasyfikator i przygotujemy testowe dane do predykcji. Dane poddamy identycznemu przygotowaniu jak dane treningowe.
best_clf = classifiers[1][1]
test_data = pd.read_csv("data/test.csv")
dummies = pd.get_dummies(test_data['Sex'], prefix='Sex', prefix_sep='-')
test_data = pd.concat([test_data, dummies], axis=1)
dummies = pd.get_dummies(test_data['Embarked'], prefix='Embarked', prefix_sep='-')
test_data = pd.concat([test_data, dummies], axis=1)
test_data.drop(['Sex','Embarked'], axis=1, inplace=True)
test_data['Fare'].fillna(test_data['Fare'].median(), inplace=True)
age_medians = test_data.groupby(['Parch', 'SibSp'])['Age'].median()
age_median = test_data['Age'].median()
for i, row in test_data.iterrows():
if row['Age'] != row['Age']:
guess_age = age_medians[row['Parch'],row['SibSp']]
if guess_age != guess_age:
guess_age = age_median
test_data.at[i, 'Age'] = guess_age
idx = test_data['PassengerId']
test_data.drop(['PassengerId','Name','Ticket','Cabin'], axis=1, inplace=True)
test_data.drop(['Sex-male'], axis=1, inplace=True)
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
to_scale = ['Fare','Pclass','Age','Parch','SibSp']
test_data[to_scale] = scaler.fit_transform(test_data[to_scale])
W zmiennej idx został zapisany index z listy pasażerów zbioru testowego. Będzie on nam potrzebny do przygotowania pliku csv, który wyślemy do sprawdzenia przez Kaggle. Tym razem nasz klasyfikator trenujemy na pełnym zbiorze treningowym.
train_data_f = train_data.iloc[:,1:] train_data_l = train_data.iloc[:,0] best_clf.fit(train_data_f, train_data_l)
Wykonujemy próbę przewidywania dla zbioru testowego i przygotowujemy plik do wysłania w celu oceny skuteczności użytego algorytmu klasyfikacji.
test_prediction = best_clf.predict(test_data)
out = pd.concat([idx,pd.Series(test_prediction.astype(int))], axis=1)
out.rename(columns={0: 'Survived'}, inplace=True)
out.to_csv("data/predictions_gbc.csv", index=False, header=True)
Osiągnięta dokładność dla danych testowych wyniosła ~0.77 , czyli w 77 na 100 przypadkach prawidłowo określiliśmy czy pasażer zbioru testowego przeżył katastrofę. Oczywiście są lepsze wyniki, nawet 100%, ale taka dokładność nie wydaje się być wynikiem jakości algorytmów. Takie wysokie wyniki wynikają z tego, że ktoś „oszukiwał” znając pełne dane zbioru testowego, lub miał bardzo dużo szczęścia. Jeżeli macie wolny czas też możecie spróbować szczęścia uwzględniając w predykcji czynnik losowy.
test_prediction = best_clf.predict_proba(test_data)
test_prediction_ = np.array(())
for p in test_prediction[:,0]:
if p > np.random.random():
test_prediction_ = np.append(test_prediction_,0)
else:
test_prediction_ = np.append(test_prediction_,1)
out = pd.concat([idx,pd.Series(test_prediction_.astype(int))], axis=1)
out.rename(columns={0: 'Survived'}, inplace=True)
out.to_csv("data/predictions_gbc_proba.csv", index=False, header=True)
Pamiętajcie tylko, że Kaggle daje możliwość sprawdzenia do 10 plików wynikowych na 24h 🙂