Opis rozwiązania, jakże ambitnego problemu, balansowania kijem na ruchomej platformie z wykorzystaniem sieci neuronowej do gromadzenia wiedzy przez agenta. Całość opisywanego kodu napisanego w Python3.5 znajduje się w repozytorium GitHub pod adresem: https://github.com/majchernet/RL_CartPole-with-neural-network. Środowisko opisujące ten problem pochodzi z siłowni OpenAI (http://gym.openai.com/envs/#classic_control).
Środowisko zdefiniowane zostało w płaskiej przestrzeni, a sama platforma może być poruszana po poziomej linii w lewo lub w prawo. Zadanie rozpoczynamy z kijem ustawionym w pozycji zbliżonej do pionu. Naszym celem jest stworzyć algorytm, który na podstawie obserwacji środowiska będzie tak poruszał platformą, aby nie dopuścić do upadku kija. Eksperyment kończy się jeżeli kij będzie miał odchylenie od pionu przekraczające 15 stopni lub platforma przesunie się na zbyt dużą odległość od środka – wartość współrzędnej położenia jest definiowana przez środowisko. Za każdy krok czasowy, kiedy pozostajemy w grze otrzymujemy „nagrodę” w wysokości 1 punktu. Eksperyment kończy się sukcesem, jeżeli uzbieramy 199 punktów. Uznajemy, że algorytm zdał zadanie, jeśli średnia ze 100 ostatnich prób wynosi 199, czyli nie popełnił w 100 próbach żadnego błędu.
Otrzymywanie nagród za każdy kolejny krok czasowy przed „game over” powoduje, że jest to modelowy problem uczenia ze wzmacnianiem (reinforcement learning), gdzie agent podejmuje decyzje na podstawie obserwacji środowiska. Agent obserwuje środowisko i na tej podstawie podejmuje akcję, przekazuje ją do środowiska, które zwraca mu kolejny stan środowiska wraz z wartością otrzymanej nagrody za podjęte działanie (i tak dalej w pętli). W uproszczeni wygląda to jak na schemacie poniżej.

Tak więc mamy w środowisku określone:
- przestrzeń stanów, które obserwuje agent, w tym wypadku jest to przestrzeń ciągła na ile ciągłą może być przestrzeń w systemie binarnym o ograniczonych zasobach i precyzji,
- przestrzeń możliwych akcji agenta, tj. porusz platformę w lewo lub w prawo,
- funkcje przejścia pomiędzy stanami jako prawdopodobieństwo znalezienia się w stanie s’ w przypadku podjęcia przez agenta akcji a w stanie s,
- funkcje nagrody natychmiastowej jaką otrzymuje agent przy zmianie stanu środowiska ze stanu s do s’ po podjęciu akcji a, w naszym przypadku zawsze jeden punkt, jeżeli agent nie osiągnął stanu terminującego epizod.
Przestrzeń możliwych stanów środowiska CartPole-v0 jest ciągła i opisana przez 4 współrzędne a przestrzeń akcji jest dyskretna i zawiera jedynie dwie wartości.
Python 3.5.3 (default, Jan 19 2017, 16:11:04)
[GCC 6.3.0 20170118] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import gym
>>> env = gym.make('CartPole-v0')
>>> print(env.observation_space)
Box(4,)
>>> print(env.action_space)
Discrete(2)
Zakres wartości jakie mogą przybierać współrzędne w przestrzeni stanów to:
>>> print(env.observation_space.high) [ 4.80000000e+00 3.40282347e+38 4.18879020e-01 3.40282347e+38] >>> print(env.observation_space.low) [ -4.80000000e+00 -3.40282347e+38 -4.18879020e-01 -3.40282347e+38]
Są to odpowiednio w kolejności:
- położenie platformy,
- prędkość platformy,
- kąt odchylenia kija,
- prędkość górnej końcówki kija.
Przestrzeń akcji zdefiniowana jest jako (jakby to politycznie nie zabrzmiało):
- 0 – przesuń platformę w lewo
- 1 – przesuń platformę w prawo
Uruchomiony program działa w pętli 100 (NR) powtórzeń eksperymentu. W każdym z powtórzeń eksperymentu nauka balansowania jest rozpoczyna od „zera”, w każdym powtórzeniu eksperymentu mamy 2000 (NE) epizodów/prób – (dalej w artykule określenie epizod i próba będą używane zamiennie), w ciągu których mamy nauczyć agenta wykonywania zadania. Na początku każdego eksperymentu deklarujemy „czystą”, nie skażoną wiedzą sieć neuronową, którą będziemy nasączać umiejętnościami odpowiedniego zachowania.
# Neural Network to store knowledge nn = NN([4,5,2])
Sieć jest zdefiniowana przez obiekt klasy NN, definicja uniwersalnej klasy znajduje się w pliku nn.py. Model sieci, opisywany krótko w poprzednim wpisie na blogu, wykorzystuje Googlową bibliotekę TensorFlow. W naszym wypadku sieć ma 4 węzły wejściowe, po jednym dla każdej ze współrzędnych obserwowanego środowiska, pięć węzłów w jednej warstwie ukrytej i dwa węzły wyjściowe, jeden z nich ma być aktywowany dla ruchu w lewo drugi dla ruchu w prawo. Do uruchomienia epizodu/próby w eksperymencie używana jest funkcja:
def runEpisode(env, T, eve, episodeNumber, render = False)
Jako argumenty funkcji przekazujemy kolejno:
- env – odnośnik do naszego środowiska,
- T – maksymalną ilość kroków w próbie,
- exploreRate – wartość opisująca współczynnik „explore vs exploit”,
- i – numer próby w eksperymencie,
- render – zmienna określająca czy wizualizować przebieg eksperymentu.
Bardzo ważnym elementem w uczeniu ze wzmacnianiem jest tu czynnik „explore vs exploit” (w używanym przeze mnie skrócie eve – nie wiem czy i jakie ma ten termin tłumaczenie na język polski, eksploracja konta wykorzystanie?). Generalnie, czynnik decyduje o tym czy agent mam wykonywać losowe akcje przez co eksplorować środowisko i odkrywać jego nowe stany, czy podejmować zapamiętane i znane akcje, które dają mu najwyższą możliwość wynagrodzenia. Szczegółowo, podejście i strategie maksymalizacji nagrody przez odpowiednie dobierania czynnika eve są opisane w klasycznym (ten klasyczny jakoś dziwnie brzmi w kontekście informatyki) problemie gry na wielu jednorękich bandytach https://en.wikipedia.org/wiki/Multi-armed_bandit
W naszym wypadku wartość czynnika eve ustal funkcja:
def exploreRate(i):
# minimal explore vs exploit rate
global minimalEve, exploreResults
if fixedEve:
return minimalEve
# Forece explore througt first 100 tries
if i < 100:
return 1
# calculate eve value based on recent tries results and number of episode
rateLastNTry = 1 - (sum(exploreResults[-lastNTry:])/lastNTry)*(1.0/T)
rateStep = 1 - i * (1/NE)
rate = (2*rateLastNTry + 8*rateStep) / 10
return rate if rate > minimalEve else minimalEve
do wyliczenia brane są dwie wartości, średnia uzyskanych wyników z ostatnich 100 (lastNTry) oraz numer kolejnej próby (i), czynniki uwzględniane są odpowiednio z wagami, w powyższym wypadku to 2 i 8. Czyli im lepiej sprawdza się wiedza zgromadzona w sieci neuronowej i lepiej nam balansowanie kijem wychodzi, tym bardziej jesteśmy skłonni wykorzystywać środowisko i podejmować wyuczone akcje. Podobnie im więcej mamy wykonanych prób za sobą, tym mniej eksplorujemy. Pozostawiona jest pewna minimalna większa od zera możliwa wielkość dla eve. Funkcja zwraca wartość z zakresu <0,1> 1 – oznacza eksplorację, 0 – wykorzystanie czyli odpytanie sieci neuronowej o najlepszą dla danego stanu akcję.
if eve > np.random.random(): #random explore
action = env.action_space.sample()
else: # get best action for curent state
action = np.argmax(nn.ask([observation]))
Całość teorii podejmowania decyzji w uczeniu wzmocnionym znana jest pod nazwą MDP (Markov Decision Process), a w sieci można znaleźć wiele artykułów wyjaśniających ją w najdrobniejszych szczegółach. Dokładniejsze jej opisywanie tutaj sprowadziło by się do zadania przetłumaczenia tych artykułów, na co nie mam obecnie czasu i ochoty.
W uproszczeniu, idea uczenia wzmocnionego została zaimplementowana w następujący sposób, początkowo poruszamy się losowo i obserwujemy po jakim ruchu dla danego stanu udało nam się dostać nagrody. Oczywiście nie bierzemy pod uwagę jedynie natychmiastowej nagrody, którą dostaliśmy po wykonaniu działania na środowisku, ale wszystkie nagrody które otrzymaliśmy do zakończenia próby od wykonania danego ruchu. Jak to możliwe że wiemy co będzie dalej, po wykonaniu ruchu? Zliczanie otrzymanych nagród za poszczególne kroki w epizodzie dokonujemy dopiero po jego zakończeniu. W zmiennej
episodeStates = []
zapamiętujemy wszystkie kroki w próbie, stany środowiska w kolejnych krokach, pojętą po ich obserwacji akcję, natychmiastową uzyskaną nagrodę w kroku, całkowitą uzyskaną nagrodę od kroku do końca próby. Nagroda całkowita od kroku do końca próby obliczana jest wraz ze współczynnikiem
discountRate = 0.98
który odpowiednio pomniejsza nagrodę w kolejnych krokach czasowych, inaczej mówiąc, ograniczamy nieskończoność horyzontu zdarzeń, które mają znaczenie. Wyliczone dane dopisujemy do tablicy wszystkich stanów, które osiągnęliśmy w kolejnych epizodach w ramach eksperymentu.
if done:
# backward calculate rewards for episode
for move in range(len (episodeStates)-1,0,-1):
update = episodeStates[move][3] * discountRate ** (len (episodeStates)-1-move)
if (update > minimalUpdate): #minimal update that matter
totalReward += update
# add totalreward to states table
episodeStates[move].append(totalReward)
episodeStates[move].append(episodeNumber)
allStates.append(episodeStates[move])
Do gromadzenia i pamiętania wiedzy przez agenta na temat podejmowanych decyzji, wykorzystana została wspominana sieć neuronowa. Agent przez pierwsze 100 prób porusza się zupełnie losowo, funkcja exploreRate zwraca 1:
# Forece explore througt first 100 tries
if i < 100:
return 1
Po 100 epizodach kolejne próby kończone są procesem uczenia sieci neuronowej. Po każdej próbie powyżej 100, bierzemy wynik ostatnich 10000 zapamiętanych stanów z ostatnich prób i podjętych dla nich decyzji, sortujemy jej po uzyskanej całkowitej nagrodzie. Pierwszy 1000 z najlepszym uzyskanym wynikiem używamy do uczenia sieci neuronowej. Do uczenia sieci konwertujemy jeszcze do listy dwuelementowych wektorów podjęte akcje (0 lub 1), ponieważ nasza sieć ma dwa węzły wyjściowe.
# take 10k last sates
del allStates[:-10000]
# and sort them by total obtained reward
allStatesSorted = sorted (allStates, key=lambda x: x[4])
# take best 1k resul
X = [row[1] for row in allStatesSorted[-1000:]]
Y = [row[2] for row in allStatesSorted[-1000:]]
# Y is a list that contains 0 or 1 for made movements
# convert Y to vectors list, becouse neural network has two output nodes (for move left or right)
Y_ = []
for y in Y:
if y == 0:
Y_.append([1,0])
else:
Y_.append([0,1])
# train neural network model
nn.train(X,Y_)
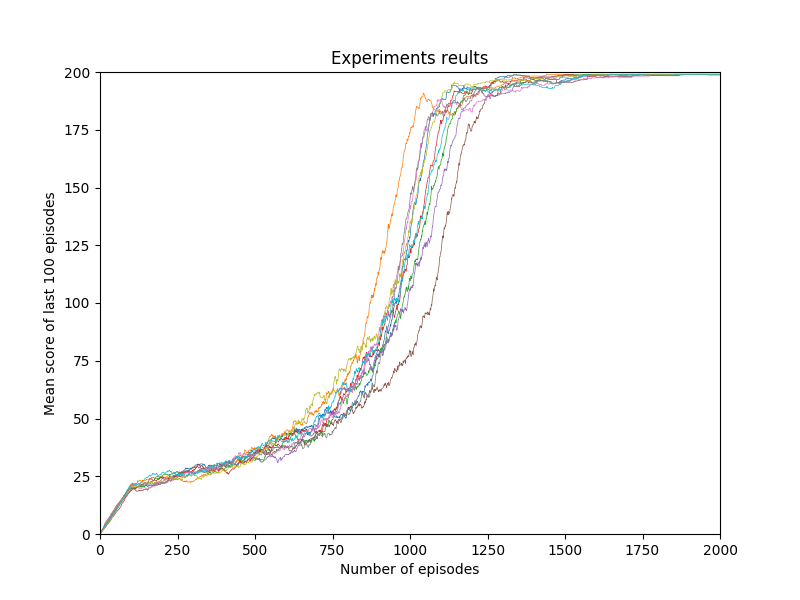
W pliku plots.py znajdują funkcje wizualizujące osiągane wyniki i przebieg kolejnych uruchomień eksperymentu. Przykładowy wynik po 10 iteracjach wygląda następująco:
i w działaniu:
I w sumie tu dopiero może się zacząć prawdziwa zabawa z tym problemem, czyli strojenie parametrów i obserwowanie ich wpływu na przebieg eksperymentu.